The orbital elements are six independent parameters that describe the shape and orientation of a Spacecraft's orbit. The orbital element systems available in FreeFlyer are described below. The ElementConvert function can be used to convert orbital elements between the different systems.
FreeFlyer supports the following orbit element types, described on this page:
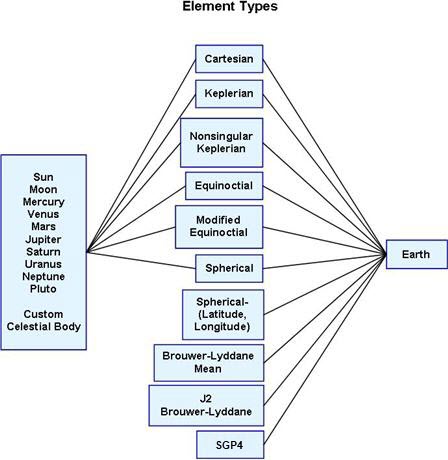
The diagram below illustrates the orbital element systems that are available for each central body in FreeFlyer. Note that the Spherical (Latitude, Longitude), Brouwer-Lyddane Mean, J2 Brouwer-Lyddane, and SGP4 elements are intended for use only when the Spacecraft's central body is Earth.
The Cartesian element set defines the position and velocity of a Spacecraft with respect to the origin of an inertial rectangular coordinate system. Positions and velocities are expressed by their components along the three principal axes of the ICRF reference frame.
Element |
Description |
X |
Position along the X-axis |
Y |
Position along the Y-axis |
Z |
Position along the Z-axis |
VX |
Velocity along the X-axis |
VY |
Velocity along the Y-axis |
VZ |
Velocity along the Y-axis |
// Assign values to the Cartesian orbital elements with respect to the ICRF frame Spacecraft1.X = -3410.673; Spacecraft1.Y = 5950.957; Spacecraft1.Z = -1788.627; Spacecraft1.VX = 1.893; Spacecraft1.VY = -1.071; Spacecraft1.VZ = -7.176; |
You can also set and get a Spacecraft's or CelestialObject's Cartesian state with respect to other reference frames using the methods:
•Spacecraft.SetCartesianState() and Spacecraft.GetCartesianState() •CelestialObject.SetCartesianState() and CelestialObject.GetCartesianStateAtEpoch() |
The Keplerian element set defines six parameters that describe the shape, size, and orientation of a Spacecraft's orbit, as well as the Spacecraft's current location in the orbit (represented by the True Anomaly). The Keplerian element set assumes perfect Keplerian orbital motion, so all gravitational forces are treated as point masses and no perturbing forces are considered when calculating these parameters.
Element |
Description |
A |
Semi-major axis |
E |
Eccentricity |
I |
Inclination |
RAAN |
Right Ascension of the Ascending Node |
W |
Argument of Periapsis |
TA |
True Anomaly |
// Assign values to the Keplerian orbital elements with respect to the ICRF frame Spacecraft1.A = 7088.42; Spacecraft1.E = 5.17E-08; Spacecraft1.I = 98.22; Spacecraft1.RAAN = 301.97; Spacecraft1.W = 310.24; Spacecraft1.TA = 244.52; |
You can also set and get a Spacecraft's or CelestialObject's Keplerian state with respect to other reference frames using the methods:
•Spacecraft.SetKeplerianState() and Spacecraft.GetKeplerianState() •CelestialObject.SetKeplerianState() and CelestialObject.GetKeplerianStateAtEpoch() |
The spherical element set defines the position and velocity of a Spacecraft with respect to the ICRF reference frame in spherical coordinates.
Element |
Description |
Radius |
Magnitude of the position vector |
RA |
Right Ascension |
DEC |
Declination |
Vi |
Magnitude of the velocity vector |
Azimuth |
Velocity azimuth angle |
VFPA |
Vertical Flight Path Angle |
// Assign values to the Spherical orbital elements Spacecraft1.SphericalRadius = 7088.42; Spacecraft1.RA = 119.81; Spacecraft1.DEC = -14.61; Spacecraft1.Vi = 7.498; Spacecraft1.SphericalAzimuth = 188.50; Spacecraft1.VerticalFPA = 90.00; |
Spherical (Latitude, Longitude)
The spherical element set defines the position and velocity of a Spacecraft with respect to the Earth Fixed in spherical coordinates, using the Earth's latitude and longitude in place of right ascension and declination. This element set is intended for use only when the Spacecraft's central body is Earth.
Element |
Description |
Radius |
Magnitude of the position vector |
Latitude |
Geodetic latitude of the spacecraft's subsatellite point |
Longitude |
Longitude of the spacecraft's subsatellite point |
Vi |
Magnitude of the velocity vector |
Azimuth |
Velocity azimuth angle |
HFPA |
Horizontal Flight Path Angle |
// Assign values to the Spherical Latitude/Longitude orbital elements Spacecraft1.LatLongRadius = 7088.42; Spacecraft1.Latitude = -14.72; Spacecraft1.Longitude = 64.13; Spacecraft1.LatLongVi = 7.58; Spacecraft1.LatLongAzimuth = 192.29; Spacecraft1.HorizontalFPA = 0; |
A representation of the Keplerian element set which removes the mathematical singularities at E = 0 and I = 0 degrees.
Element |
Description |
A |
Semi-major axis |
e1 |
E cos(RAAN + W) |
e2 |
E sin(RAAN + W) |
e3 |
sin(I/2) sin(RAAN) |
e4 |
sin(I/2) cos(RAAN) |
e5 |
RAAN + W + MA |
// Assign values to the Nonsingular Keplerian orbital elements Spacecraft1.NonSingularA = 7070.81; Spacecraft1.NonSingularE1 = 0.00181; Spacecraft1.NonSingularE2 = -0.00170; Spacecraft1.NonSingularE3 = -0.641; Spacecraft1.NonSingularE4 = 0.400; Spacecraft1.NonSingularE5 = 136.72; |
A representation of the Keplerian element set which removes the mathematical singularities at E = 0 and I = 0 and 90 degrees. This element set has a singularity at an inclination of 180 degrees.
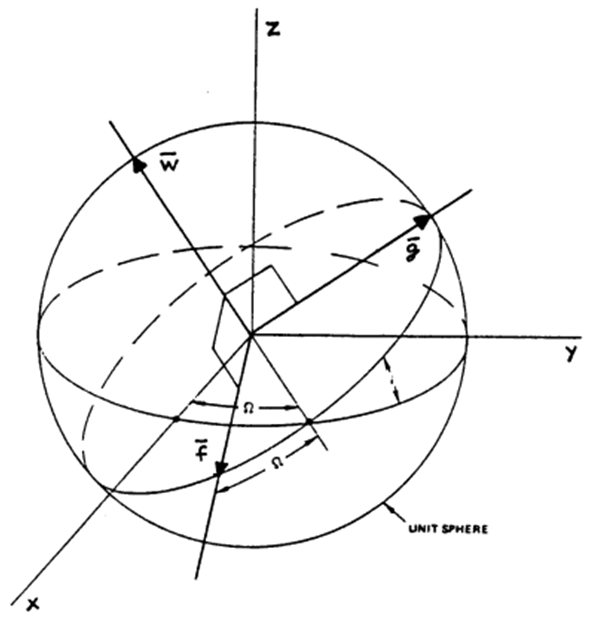
Direct Equinoctial Reference Frame
Note: The equinoctial reference frame in FreeFlyer is the direct (prograde) equinoctial reference frame.
Element |
Description |
A |
Keplerian semi-major axis |
h |
E sin(RAAN + W) |
k |
E cos(RAAN + W) |
p |
tan(I/2) sin(RAAN) |
q |
tan(I/2) cos(RAAN) |
Longitude |
Mean Longitude: RAAN + W + MA |
// Assign values to the Equinoctial orbital elements Spacecraft1.EquinoctialA = 7070.81; Spacecraft1.EquinoctialH = 0.00237; Spacecraft1.EquinoctialK = 0.000731; Spacecraft1.EquinoctialP = -0.735; Spacecraft1.EquinoctialQ = 0.458; Spacecraft1.EquinoctialLongitude = 4.412; |
A representation of the Keplerian element set which removes the mathematical singularities at E = 0 and I = 0 and 90 degrees. This element set has a singularity at an inclination of 180 degrees.
Element |
Description |
p |
A(1 - E2) |
f |
E cos(RAAN + W) |
g |
E sin(RAAN + W) |
h |
tan(I/2) cos(RAAN) |
k |
tan(I/2) sin(RAAN) |
L |
True Longitude: RAAN + W + TA |
// Assign values to the Modified Equinoctial orbital elements Spacecraft1.ModifiedEquinoctialP = 7070.766; Spacecraft1.ModifiedEquinoctialF = 0.00180; Spacecraft1.ModifiedEquinoctialG = -0.00170; Spacecraft1.ModifiedEquinoctialH = 0.610; Spacecraft1.ModifiedEquinoctialK = -0.980; Spacecraft1.ModifiedEquinoctialL = 136.64; |
Brouwer-Lyddane Mean
The Brouwer-Lyddane Mean element contains similar parameters to the traditional Keplerian elements, but represent values that are averaged over time rather than instantaneous values. These elements account for gravitational perturbations due to the J2-J5 oblateness terms. The Brouwer-Lyddane Mean element type, also referred to as Brouwer-Lyddane Long Transformation (BLLT), includes averaging the osculating elements using both short (days/weeks) and long-term periods (months/years). This element set is intended for use only when the Spacecraft's central body is Earth. Mean elements are particularly useful when designing orbits that are sensitive to gravitational perturbations.
Notes:
•Commonly referred to Brouwer-Lyddane Long Transformation (BLLT) |
Element |
Description |
A |
Mean semi-major axis |
E |
Mean eccentricity |
I |
Mean inclination |
RAAN |
Mean Right Ascension of the Ascending Node |
W |
Mean Argument of Periapsis |
MA |
Mean Anomaly |
// Assign values to the Brouwer-Lyddane Mean orbital elements Spacecraft1.BL_A = 7088.42; Spacecraft1.BL_E = 5.17E-08; Spacecraft1.BL_I = 98.22; Spacecraft1.BL_RAAN = 301.97; Spacecraft1.BL_W = 310.24; Spacecraft1.BL_MA = 244.52; |
This element set is a mean element set similar to the Brouwer-Lyddane Mean element set, but accounts for only the J2 gravitational perturbation term. The J2 Brouwer-Lyddane element type, also referred to as Brouwer-Lyddane Short Transformation (BLST), includes averaging the osculating elements using short-period terms (days/weeks). This element set is intended for use only when the Spacecraft's central body is Earth. Mean elements are particularly useful when designing orbits that are sensitive to gravitational perturbations.
Notes:
•Commonly referred to Brouwer-Lyddane Short Transformation (BLST) |
Element |
Description |
A |
J2 Mean semi-major axis |
E |
J2 Mean eccentricity |
I |
J2 Mean inclination |
RAAN |
J2 Mean Right Ascension of the Ascending Node |
W |
J2 Mean Argument of Periapsis |
MA |
J2 Mean Anomaly |
// Assign values to the J2 Brouwer-Lyddane Mean orbital elements Spacecraft1.BLJ2A = 7088.42; Spacecraft1.BLJ2E = 5.17E-08; Spacecraft1.BLJ2I = 98.22; Spacecraft1.BLJ2RAAN = 301.97; Spacecraft1.BLJ2W = 310.24; Spacecraft1.BLJ2MA = 244.52; |
The SGP4 derived elements are associated with the Two-Line Element (TLE) definitions. This element set is intended for use only when the Spacecraft's central body is Earth, and should be used with the SGP4 propagator.
Element |
Description |
I |
Mean inclination |
RAAN |
Mean Right Ascension of the Ascending Node |
E |
Mean Eccentricity |
W |
Mean Argument of Perigee |
MA |
Mean Anomaly |
N |
Mean Motion |
// Assign values to the SGP4 derived elements Spacecraft1.SGP4.I = 98.25; Spacecraft1.SGP4.RAAN = 302.04; Spacecraft1.SGP4.E = 0.00264; Spacecraft1.SGP4.W = 357.18; Spacecraft1.SGP4.MA = 197.55; Spacecraft1.SGP4.MeanMotion = 14.61; |
See Also